Задаволены

• крокі

Трыганаметрычныя раўнанне змяшчае адну або некалькі трыганаметрычных функцый зменнай «х» (ці любы іншы зменнай). Рашэнне трыганаметрычных ураўненняў - гэта знаходжанне такога значэння «х», якое задавальняе функцыі (функцый) і раўнанні ў цэлым.

• Рашэння трыганаметрычных ураўненняў выяўляюцца ў градусах ці радыянах. прыклады:

х = π / 3; х = 5π / 6; х = 3π / 2; х = 45 градусаў; х = 37,12 градусаў; х = 178,37 градусаў.

• Заўвага: значэння трыганаметрычных функцый ад кутоў, выяўленых у радыянах, і ад кутоў, выяўленых у градусах, роўныя. Трыганаметрычныя акружнасць з радыусам, роўным адзінцы, служыць для апісання трыганаметрычных функцый, а таксама для праверкі правільнасці рашэння асноўных трыганаметрычных ураўненняў і няроўнасцей.
• Прыклады трыганаметрычных раўнанняў:
  • sin x + sin 2x = 1/2; tg x + ctg x = 1,732;
  • cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1.

1. Трыганаметрычныя акружнасць з радыусам, роўным адзінцы (адзінкавая акружнасць).
   • Гэта акружнасць з радыусам, роўным адзінцы, і цэнтрам у пункце O. Адзінкавая акружнасць апісвае 4 асноўныя трыганаметрычныя функцыі зменнай «х», дзе «х» - кут, адлічваецца ад станоўчага напрамкі восі Х супраць гадзінны стрэлкі.
   • Калі «х» - некаторы кут на адзінкавай акружнасці, то:
   • Гарызантальная вось OAх вызначае функцыю F (х) = соs х.
   • Вертыкальная вось OВy вызначае функцыю F (х) = sin х.
   • Вертыкальная вось AT вызначае функцыю F (х) = tg х.
   • Гарызантальная вось BU вызначае функцыю F (х) = сtg х.

• Адзінкавая акружнасць таксама ўжываецца пры вырашэнні асноўных трыганаметрычных ураўненняў і няроўнасцей (на ёй разглядаюцца розныя становішча «х»).

крокі

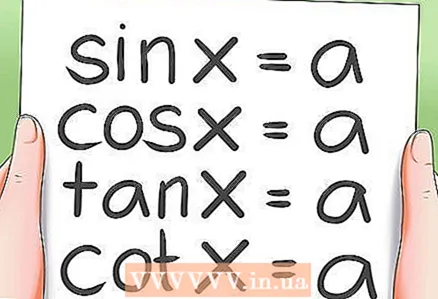1. 1 Канцэпцыя рашэння трыганаметрычных ураўненняў.
   • Для вырашэння трыганаметрычныя ўраўненні ператварыце яго ў адно або некалькі асноўных трыганаметрычных ураўненняў. Рашэнне трыганаметрычных ўраўненні ў канчатковым выніку зводзіцца да вырашэння чатырох асноўных трыганаметрычных ураўненняў.
2. 2 Рашэнне асноўных трыганаметрычных ураўненняў.
   • Існуюць 4 віды асноўных трыганаметрычных раўнанняў:
   • sin x = a; cos x = a
   • tg x = a; ctg x = a
   • Рашэнне асноўных трыганаметрычных ураўненняў мае на ўвазе разгляд розных палажэнняў «х» на адзінкавай акружнасці, а таксама выкарыстанне табліцы пераўтварэння (або калькулятара).
   • Прыклад 1. sin x = 0,866. Выкарыстоўваючы табліцу пераўтварэння (або калькулятар), вы атрымаеце адказ: х = π / 3. Адзінкавая акружнасць дае яшчэ адзін адказ: 2π / 3. Запомніце: усе трыганаметрычныя функцыі з'яўляюцца перыядычнымі, гэта значыць іх значэння паўтараюцца. Напрыклад, перыядычнасць sin x і cos x роўная 2πn, а перыядычнасць tg x і ctg x роўная πn. Таму адказ запісваецца наступным чынам:
   • x1 = π / 3 + 2πn; x2 = 2π / 3 + 2πn.
   • Прыклад 2. соs х = -1/2. Выкарыстоўваючы табліцу пераўтварэння (або калькулятар), вы атрымаеце адказ: х = 2π / 3. Адзінкавая акружнасць дае яшчэ адзін адказ: -2π / 3.
   • x1 = 2π / 3 + 2π; х2 = -2π / 3 + 2π.
   • Прыклад 3. tg (x - π / 4) = 0.
   • Адказ: х = π / 4 + πn.
   • Прыклад 4. ctg 2x = 1,732.
   • Адказ: х = π / 12 + πn.
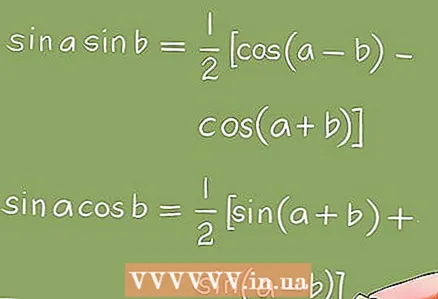3. 3 Пераўтварэнні, якія выкарыстоўваюцца пры рашэнні трыганаметрычных ураўненняў.
   • Для пераўтварэння трыганаметрычных ураўненняў выкарыстоўваюцца Алгебраічныя пераўтварэння (раскладанне на множнікі, прывядзенне аднародных членаў і г.д.) і трыганаметрычныя тоеснасці.
   • Прыклад 5. Выкарыстоўваючы трыганаметрычныя тоеснасці, раўнанне sin x + sin 2x + sin 3x = 0 пераўтворыцца ў раўнанне 4cos x * sin (3x / 2) * cos (x / 2) = 0. Такім чынам, трэба вырашыць наступныя асноўныя трыганаметрычныя ўраўненні: cos x = 0; sin (3x / 2) = 0; cos (x / 2) = 0.
     
     
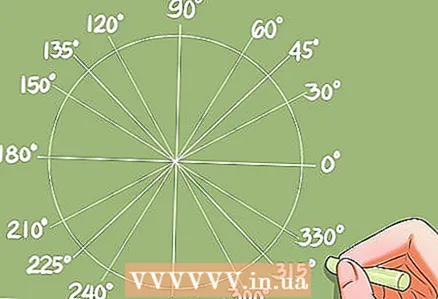
4. 4 Знаходжанне кутоў па вядомых значэнняў функцый.
   • Перад вывучэннем метадаў рашэння трыганаметрычных ураўненняў вам неабходна навучыцца знаходзіць куты па вядомых значэнняў функцый. Гэта можна зрабіць пры дапамозе табліцы пераўтварэнні або калькулятара.
   • Прыклад: соs х = 0,732. Калькулятар дасць адказ х = 42,95 градусаў. Адзінкавая акружнасць дасць дадатковыя куты, косінус якіх таксама роўны 0,732.
5. 5 Адкладзеце рашэнне на адзінкавай акружнасці.
   • Вы можаце адкласці рашэння трыганаметрычных ураўненняў на адзінкавай акружнасці. Рашэння трыганаметрычных ураўненняў на адзінкавай акружнасці ўяўляюць сабой вяршыні правільнага шматкутніка.
   • Прыклад: Рашэнні x = π / 3 + πn / 2 на адзінкавай акружнасці ўяўляюць сабой вяршыні квадрата.
   • Прыклад: Рашэнні x = π / 4 + πn / 3 на адзінкавай акружнасці ўяўляюць сабой вяршыні правільнага шасцікутнік.
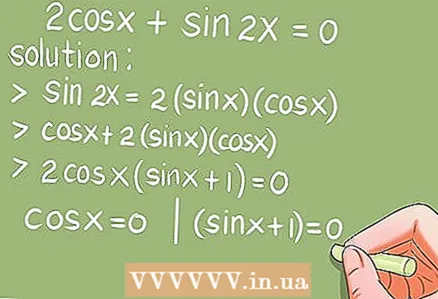6. 6 Метады рашэння трыганаметрычных ураўненняў.
   • Калі дадзенае трыганаметрычных ураўненняў ўтрымлівае ні трыганаметрычных функцый, вырашыце гэтае раўнанне як асноўнае трыганаметрычных ураўненняў.Калі дадзенае раўнанне ўключае дзве або больш трыганаметрычныя функцыі, то існуюць 2 метаду рашэння такога ўраўненні (у залежнасці ад магчымасці яго пераўтварэння).
     • Метад 1.
   • Пераўтварыце дадзенае раўнанне ў раўнанне выгляду: f (x) * g (x) * h (x) = 0, дзе f (x), g (x), h (x) - асноўныя трыганаметрычныя ўраўненні.
     
     
   • Прыклад 6. 2cos x + sin 2x = 0. (0 x 2π)
   • Рашэнне. Выкарыстоўваючы формулу падвойнага кута sin 2x = 2 * sin х * соs х, заменіце sin 2x.
   • 2соs х + 2 * sin х * соs х = 2cos х * (sin х + 1) = 0. Цяпер вырашыце два асноўных трыганаметрычных ўраўненні: соs х = 0 і (sin х + 1) = 0.
   • Прыклад 7. cos x + cos 2x + cos 3x = 0. (0 x 2π)
   • Рашэнне: Выкарыстоўваючы трыганаметрычныя тоеснасці, ператварыце дадзенае раўнанне ў раўнанне выгляду: cos 2x (2cos x + 1) = 0. Цяпер вырашыце два асноўных трыганаметрычных ўраўненні: cos 2x = 0 і (2cos x + 1) = 0.
   • Прыклад 8. sin x - sin 3x = cos 2x. (0 x 2π)
   • Рашэнне: Выкарыстоўваючы трыганаметрычныя тоеснасці, ператварыце дадзенае раўнанне ў раўнанне выгляду: -cos 2x * (2sin x + 1) = 0. Цяпер вырашыце два асноўных трыганаметрычных ўраўненні: cos 2x = 0 і (2sin x + 1) = 0.
     • Метад 2.
   • Пераўтварыце дадзенае трыганаметрычных ураўненняў у раўнанне, якое змяшчае толькі адну трыганаметрычныя функцыі. Затым заменіце гэтую трыганаметрычных функцый на некаторую невядомую, напрыклад, t (sin x = t; cos x = t; cos 2x = t, tg x = t; tg (x / 2) = t і г.д.).
   • Прыклад 9. 3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0 x 2π).
   • Рашэнне. У дадзеным раўнанні заменіце (cos ^ 2 x) на (1 - sin ^ 2 x) (паводле тоеснасці). Ператворанае раўнанне мае выгляд:
   • 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. Заменіце sin х на t. Цяпер раўнанне мае выгляд: 5t ^ 2 - 4t - 9 = 0. Гэта квадратнае раўнанне, якое мае два кораня: t1 = -1 і t2 = 9/5. Другі корань t2 ня задавальняе вобласці значэнняў функцыі (-1 sin x 1). Цяпер вырашыце: t = sin х = -1; х = 3π / 2.
   • Прыклад 10. tg x + 2 tg ^ 2 x = ctg x + 2
   • Рашэнне. Заменіце tg x на t. Перапішыце зыходнае раўнанне ў наступным выглядзе: (2t + 1) (t ^ 2 - 1) = 0. Цяпер знайдзіце t, а затым знайдзіце х для t = tg х.
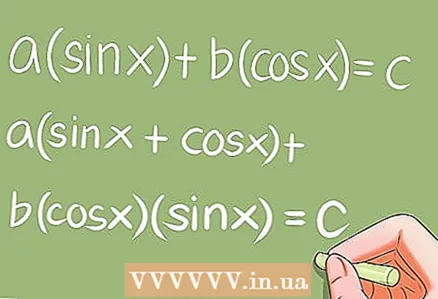7. 7 Асаблівыя трыганаметрычныя ўраўненні.
   • Ёсць некалькі асаблівых трыганаметрычных ураўненняў, якія патрабуюць канкрэтных пераўтварэнняў. прыклады:
   • a * sin x + b * cos x = c; a (sin x + cos x) + b * cos x * sin x = c;
   • a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
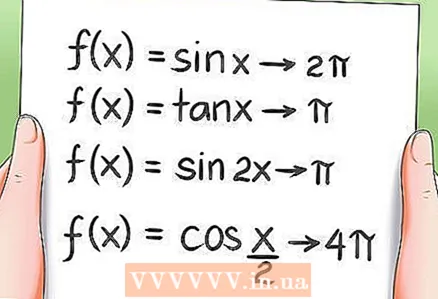8. 8 Перыядычнасць трыганаметрычных функцый.
   • Як згадвалася раней, усё трыганаметрычныя функцыі з'яўляюцца перыядычнымі, гэта значыць іх значэння паўтараюцца праз пэўны перыяд. прыклады:
     • Перыяд функцыі f (x) = sin x роўны 2π.
     • Перыяд функцыі f (x) = tg x роўны π.
     • Перыяд функцыі f (x) = sin 2x роўны π.
     • Перыяд функцыі f (x) = cos (x / 2) роўны 4π.
   • Калі перыяд паказаны ў задачы, вылічыце значэнне «х» ў межах гэтага перыяду.
   • Заўвага: рашэнне трыганаметрычных ураўненняў - няпростая задача, якая часта прыводзіць да памылак. Таму старанна правярайце адказы. Для гэтага можна выкарыстоўваць графічны калькулятар, каб пабудаваць графік дадзенага раўнання R (х) = 0. У такіх выпадках рашэнні будуць прадстаўлены ў выглядзе дзесятковых дробаў (гэта значыць π замяняецца на 3,14).